Power Flow Analysis Intro

Load flow analysis, also known as power flow analysis, is a fundamental tool used in power systems analysis to evaluate the steady-state operating characteristics of a power network. The network is represented by a series of interconnected buses, each representing a different location or node. The buses are categorized for load flow analysis depending on their characteristics and parameters.

Each bus or node in a power system is connected to four different quantities: real and reactive powers, voltage magnitude, and phase angle. Two of the four quantities are predetermined in a load flow solution, while the other two must be determined by solving the equations. The buses are divided into the following three groups according to the quantities specified:

1. Load Bus
2. Generator Bus
3. Slack Bus

---

Load Bus

Load Bus: The actual and reactive components of the power are described at the load bus. Through the load flow solution, it is wanted to determine the voltage magnitude and phase angle. At a bus like this, just P_D and Q_D are required to be specified because, at a load, bus voltage might change up to a certain percentage, for example. The voltage’s phase angle is also not particularly significant for the load.

Generator Bus

The provided details specify the magnitude of the voltage linked to the generator voltage and the real power P_G according to their ratings at the generator bus or voltage-controlled bus. In order to proceed, it is crucial to determine both the phase angle of the bus voltage and the amount of reactive power generated, denoted as Q_G.

Slack Bus

Slack, Swing, or Reference Bus: There are two types of buses in a power system: load buses and generator buses. We have defined genuine power P injectors for these buses.

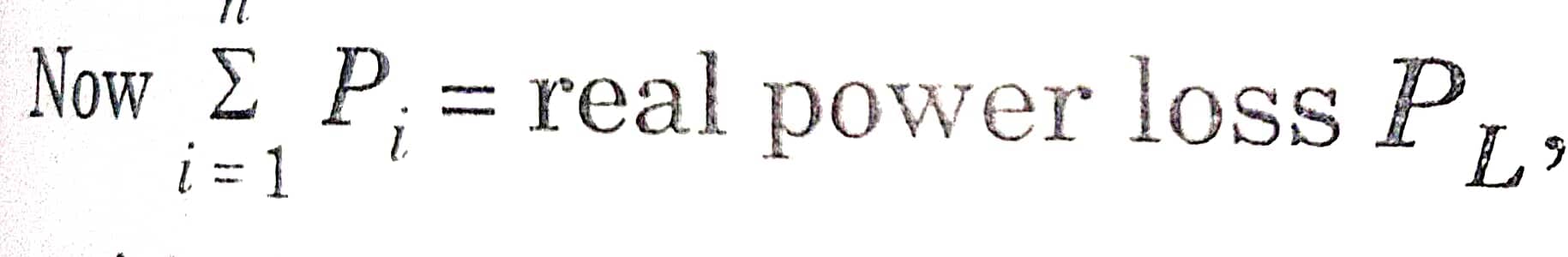
The power injection at the buses denoted as P_i, follows a positive value for generator buses and a negative value for load buses. The losses remain unknown until the load flow solution is achieved. Consequently, one of the generator buses is typically designated to absorb additional real and reactive power to compensate for gearbox losses.

This specific bus is commonly referred to as a slack or swing bus. The voltage magnitude, V, and phase angle, θ, are specified for this bus, while the real and reactive powers, P_G and Q_G, are computed using the load flow solution. The information discussed above is summarized in the table below:

Bus type	Quantities specified	Quantities to be obtained
Load bus	P, Q	|V| , δ
Generator bus	P, |V|	Q, δ
Slack bus	|V| ,δ	P, Q

Typically, the reference is the phase angle of the voltage at the slack bus. The real and reactive components of the voltage across a bus are used as independent variables for the load flow equations in the analysis that follows, i.e.

V_i∠δ_i = e_i+f_c

where the voltage at the ith bus has real and reactive components, respectively, as e_i and f_c.There are numerous additional formulations where the independent variable is either voltage, current, or both. Either the loop frame of reference or the bus frame of reference can be used to format the load flow equations. However, the nodal admittance formulation using the nodal voltages as the independent variables are the most economical from the perspective of computer time and memory.

---

Frequently Asked Question

---

Get All Study Material From Here.